Blender Python Bites #6 – Performing arbitrary transforms
Transformation matrices are a concise way to represent linear transformations in 3D space. They let you model any linear transformation you can imagine using a single 4x4 matrix.
Here’s how we can perform transformations like translate, rotate and scale along arbitrary axes using them in the Blender API. 👇🏻
Let’s assume the arbitrary axis to be a line that passes through p1 and p2, where:
import bpy
from mathutils import Matrix, Vector
p1 = Vector((1, 3, 2))
p2 = Vector((-4, -2, -7))
Subtracting p2 from p1, we get p1 -> p2 vector
direction = p2 - p1
In order to be able to use this for transformations, we need the unit vector pointing in this direction. We can get this using Vector.normalize()
direction.normalize()
Or if you don’t want to modify ‘direction’ in-place:
direction_n = direction.normalized()
Now we can use this direction vector to perform our transformations.
Let’s use the gorgeous default cube:
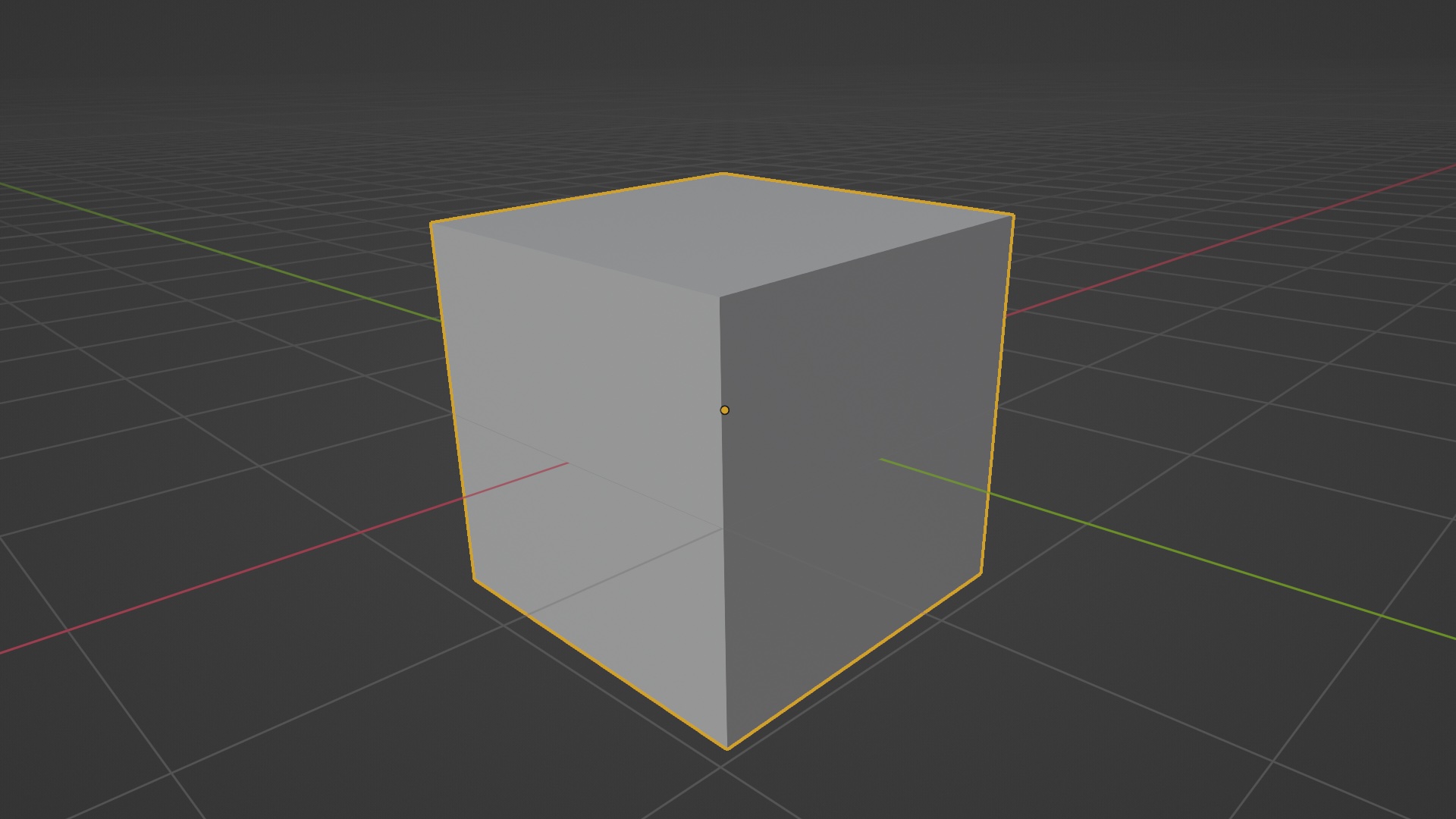
obj = bpy.data.objects['Cube']
1. Translation
To translate an object in this direction, we do:
obj.location += magnitude * direction
Where magnitude is the number of units we want to move our object along ‘direction’. E.g. To move 2 units along ‘direction’:
obj.location += 2 * direction
This would translate our cube like so:
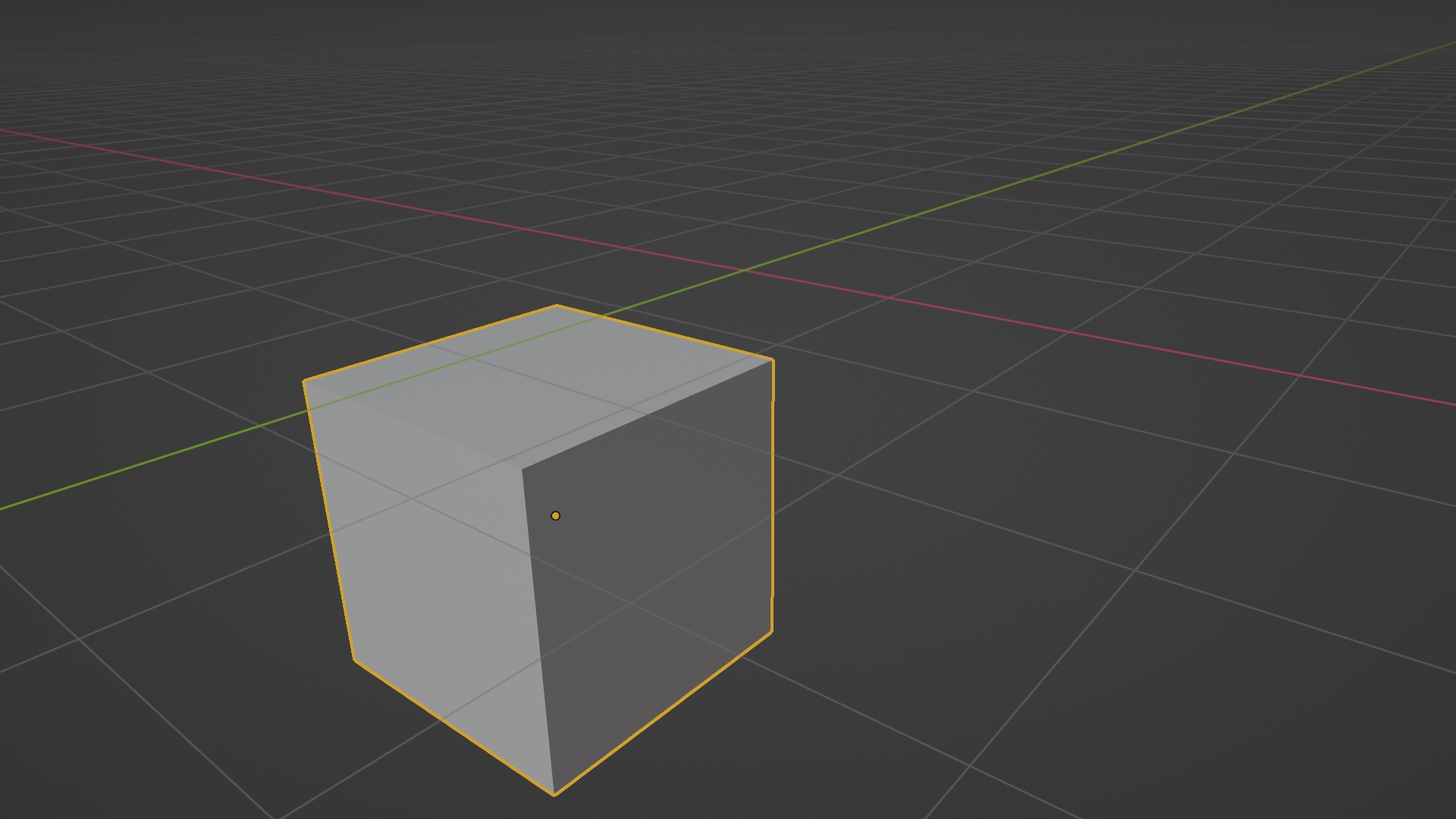
2. Rotation
To rotate an object along ‘direction’, we do:
import math
matrix_rotation = Matrix.Rotation(math.radians(30), 4, direction)
obj.matrix_world @= matrix_rotation
Where the first argument in Matrix.Rotation() is the angle of rotation (converted to radians using math.radians). This creates a transformation matrix for rotation.
The obj.matrix_world is the transformation matrix of our object in question. By doing a matrix multiplication @= of this with our rotation matrix, we can perform rotations along an arbitrary axis.
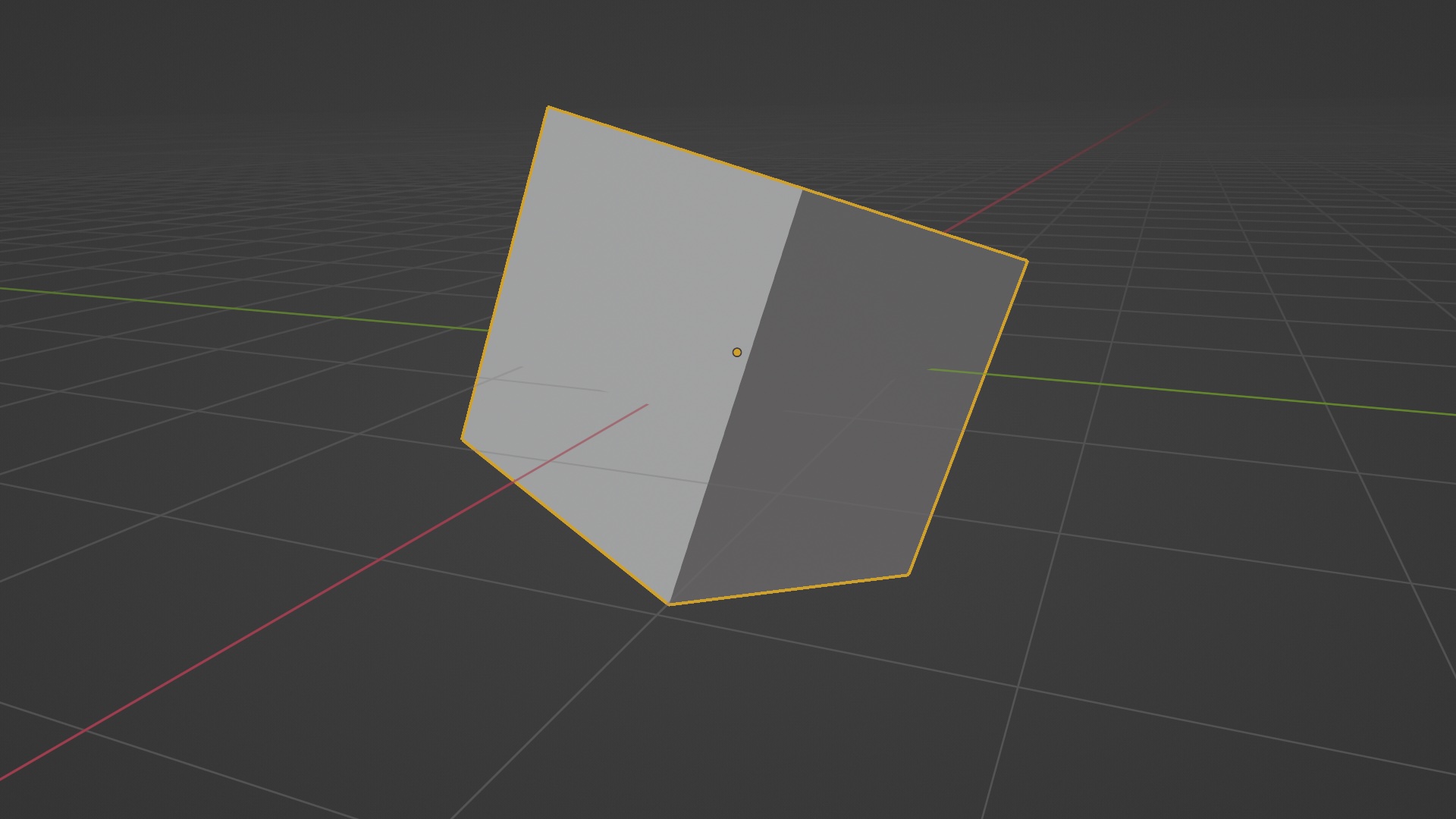
If you are running this in the Python Console directly, you can re-run the last line a few times to see how the cube rotates.
3. Scaling
To scale an object 2 units along ‘direction’, we do:
matrix_scale = Matrix.Scale(2, 4, direction)
obj.matrix_world @= matrix_scale
Where the first argument in Matrix.Scale() is the number of units by which we want to scale. The Matrix.Scale() function lets us create a transformation matrix for scaling.
But scaling an object like this wouldn’t produce the effect we imagine. Because performing a scaling transform in object mode behaves differently from translation or rotation.
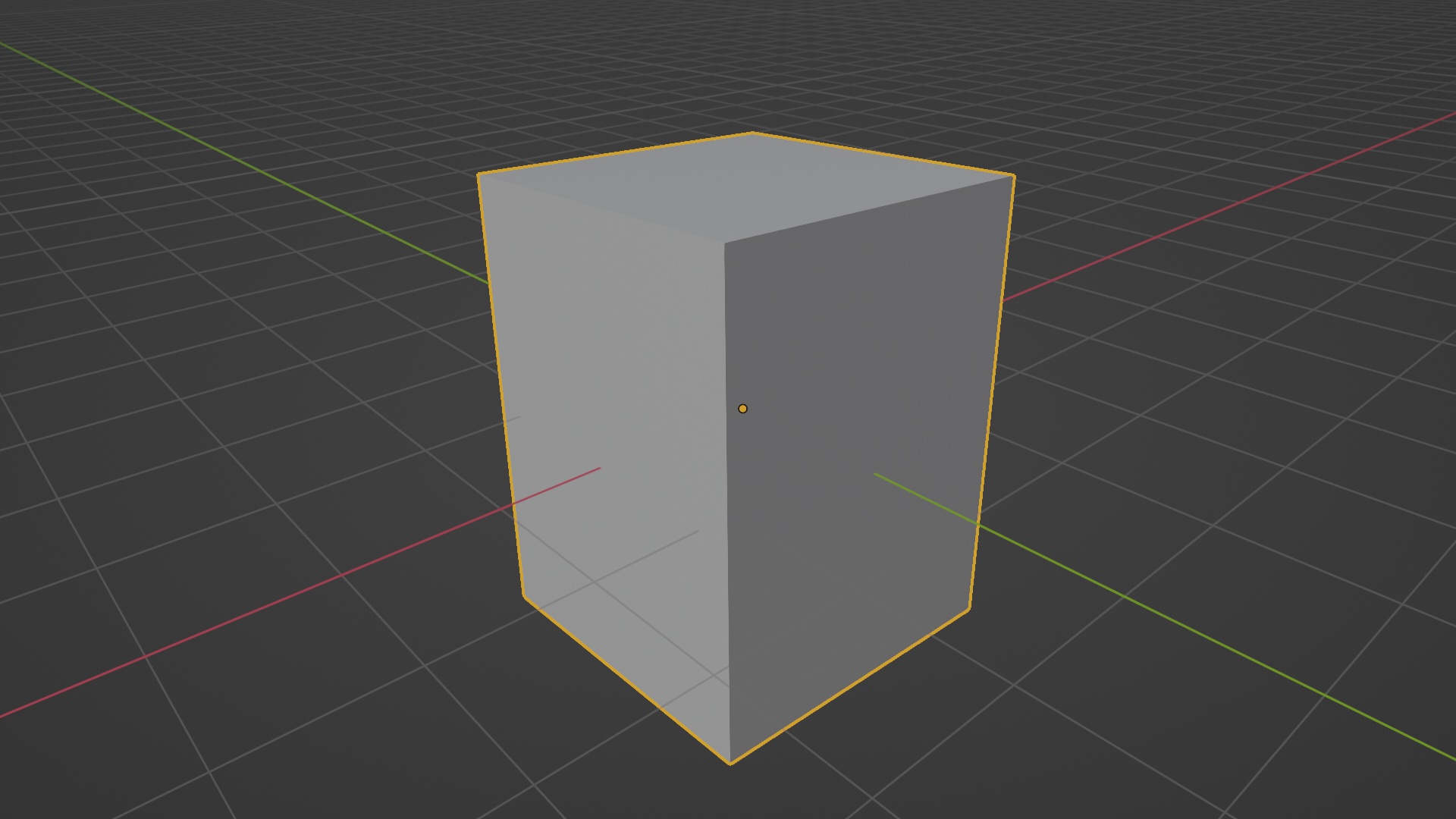
In order to get the desired effect, we can use the bmesh module
import bmesh
# Create a new BMesh object
mesh = bmesh.new()
# Add the mesh data from our object
mesh.from_mesh(obj.data)
# Apply the transform using mesh.transfor() method
mesh.transform(matrix_scale)
# Nothing would change yet, since we have to apply these tranforms
# back to our original object
mesh.to_mesh(obj.data)
# Free the BMesh object
mesh.free()
And that’s it. If you notice, our object is now scaled along our ‘direction’ vector:
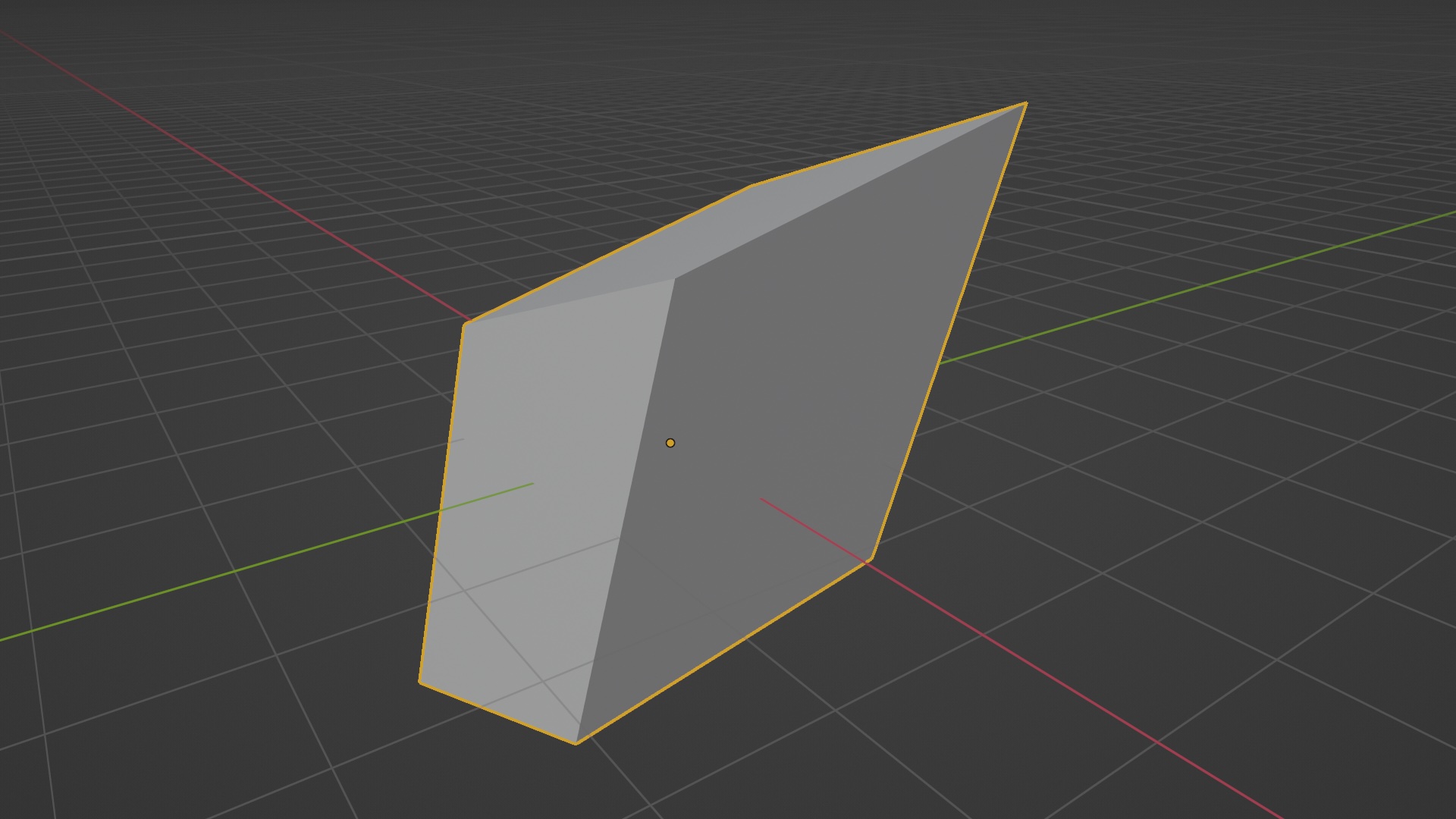
So that’s how you can perform transformations on arbitrary axes. The same can be applied to mimic tools like vertex slide and many other transforms we do in Blender.
As an exercise, see if you can implement a vertex slide operation using matrices and the bmesh module. 🙌🏻
Resources
- Linear Algebra series by 3Blue1Brown
- Mathematics for Computer Graphics book by Springer
Subscribe to my newsletter
Join 1200+ Technical Artists, Developers and CG enthusiasts who receive my latest posts on Blender, Python, Scripting and Computer Graphics directly to their inbox.