Checking if a Given Point is Inside or Outside a Mesh
When manipulating meshes or doing procedural generation using the Blender Python API, there comes a time when you would want to determine if a particular point in space is inside or outside a mesh. It might be easy to predict this when you are looking at a point and a mesh visually, but how do you determine if a point is inside or outside a given mesh programmatically?
Let’s see how we can achieve this using the Blender API.
Vectors, Object Space and Closest Point
First things first, let’s think about the problem mathematically before diving into code. Basically, we have one of two possibilities: The point is either inside or outside the mesh. There is a third possibility that it could be exactly on the surface, but let’s ignore that for now. Have a look at the following diagram:
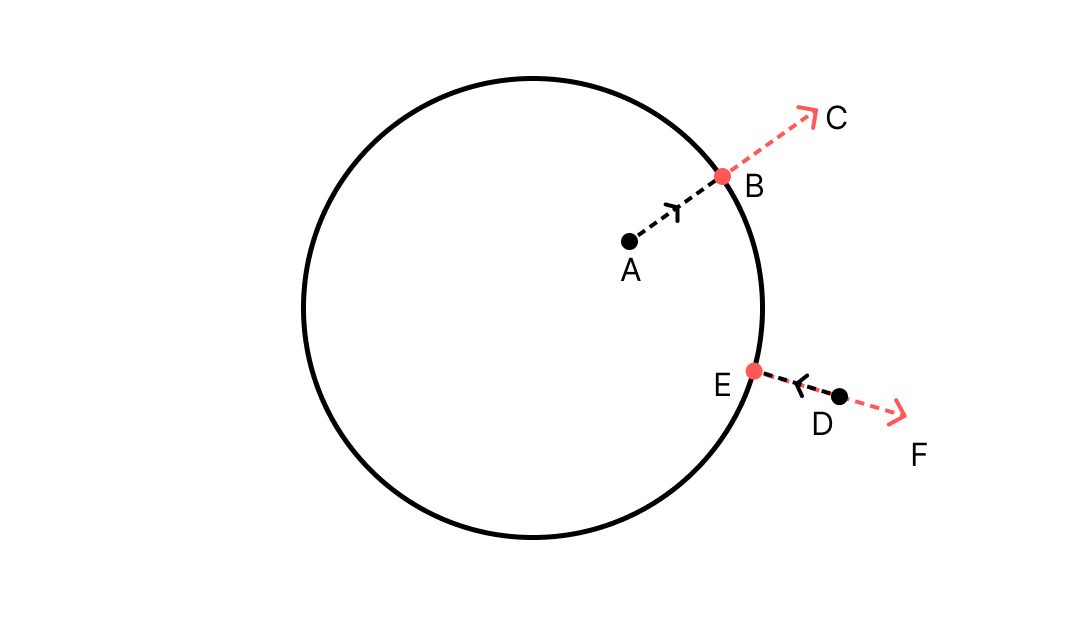
We have point A that is inside the circle, and point D that is outside the circle. The points B and E denote the closest point on the circle to points A and D respectively. The lines BC and EF are the surface normals at the points B and E respectively.
If you notice, for point A, that is inside the circle, the lines AB and BC point in the same direction. This is true for any point inside the circle. Similarly, for point D that is outside the circle, the lines DE and EF point in opposite directions. This is true for any point outside the circle.
Basically, these two rules enable us to determine if a point is inside or outside a given mesh. Now that we have a mathematical model, let’s think about how to implement this using the API.
We have three problems to solve:
- Finding the closest point on the mesh to a given point
- Finding the surface normal at this closest point
- Determine if both of them point in the same or opposite direction
For problems 1 and 2, Blender has a direct solution through the closest_point_on_mesh() method. This method can be called from any object, including meshes created from curve extrusions, NURBS surfaces, etc. This method takes a point as input and returns four things:
-
result– a boolean value that is True if a closest point is found and False otherwise -
location– a mathutils.Vector object denoting the location on the object closest to the point -
normal– a mathutils.Vector object denoting the surface normal at the closest point -
index– an int value denoting the index of the face where the closest point was found
One thing to note here is that the point that this method takes as an input has to be provided in object space. Basically that means, the coordinates of the point you provide as input should be with reference to the object; not the origin. When you get the location of an object using the API (or by looking at the properties panel), the coordinates are with respect to the origin, aka. world space.
For example, consider a scene like this:
Here, both the suzanne and the empty are sitting somewhere above the grid floor. I get their respective locations like:
>>> bpy.data.objects['Suzanne'].location
# Vector((-0.8009814620018005, 0.9618351459503174, 4.1569132804870605))
>>> bpy.data.objects['Empty'].location
# Vector((-0.500006914138794, 0.2223377823829651, 4.817152976989746))
Both of these returned values are with respect to the origin. In order to get the coordinated of a point in object space, we simply have to subtract the location of the object (with respect to which we need the coordinates) from the point in question. Assuming the location of the empty is the point you want to check if it’s inside or outside the mesh (Suzanne), you would simply do:
>>> loc_point = bpy.data.objects['Empty'].location
>>> loc_mesh = bpy.data.objects['Suzanne'].location
>>> loc_point - loc_mesh
# Vector((0.3009745478630066, -0.7394973635673523, 0.6602396965026855))
Subtracting the location of the mesh from the point in question thus would basically give us the coordinates of the point in object space.
Now that we got the coordinates of the point in object space, let’s pass it on the the closest_point_on_mesh() and see what happens:
>>> bpy.data.objects['Suzanne'].closest_point_on_mesh(loc_point - loc_mesh)
# (True, Vector((0.33592677116394043, -0.7744495868682861, 0.6882014870643616)), Vector((0.6154574751853943, -0.6154574751853943, 0.4923659861087799)), 86)
We can see that it returns a tuple of four values that correspond to the ones we discussed above.
- First, there is a boolean value True, which means that a closest point was found successfully.
- Second, there is a Vector denoting the closest point on the mesh surface to our input point
- Third, there is a Vector denoting the surface normal at this closest point on the mesh
- Fourth, there is an integer denoting the index of the face where the closest point was found
Since the first and the last values are not needed in out case, I am gonna store the required values like so:
_, closest, normal, _ = bpy.data.objects['Suzanne'].closest_point_on_mesh(loc_point - loc_mesh)
With the second and third value in the tuple, we have successfully solved the problems 1 and 2. Now the only remaining thing is to figure out is if the direction of the line drawn from our input point to the closest point on the mesh and the surface normal face in the same direction.
Again, we need to think about this mathematically before we can write code. Because, it might be easy to say by looking at our first diagram, but how do we determine this mathematically.
Let’s ponder over some high-school math again. 🙂
Similarity of direction and the Dot product
In Vector Algebra, there is a concept called dot product. If you read up the definitions, they would something like ‘product of the magnitudes of the two vectors and the cosine of the angle between them.’ Okay, what am I supposed to do with that?
That might sound unrelatable to the problem at hand, but fundamentally, dot product is a method that will allow us to measure how similar the direction of two vectors are. There are three possibilities when we do a dot product: it could be positive, zero or negative.
- If dot product is positive, they face in a similar direction (< 90 degrees apart).
- If it is zero, they are exactly perpendicular (= 90 degrees apart).
- If it is negative, the face quite opposite directions. (> 90 degrees apart)
Since all mesh objects are an approximation of curved surfaces using finely divided polygons, the two vectors that we want to evaluate will almost never face in the same (or exactly opposite) direction (except for simple primitives like a cube). There’s gonna be some difference in their directions.
In order to account for this, we can consider that the point is outside if the dot product is negative, i.e., more than 90 degrees apart and is inside when the dot product is positive, i.e., less than 90 degrees apart.
Now, that we have concluded this, let’s implement the same using the API. In Blender, to find the dot product of two vectors, vector_a and vector_b, we simply do vector_a.dot(vector_b).
So, in our case, vector_a is the vector from our input point to the closest point on the mesh. Let’s call it direction maybe:
>>> direction = closest - loc_point
And vector_b is simply the normal vector we got in the previous step. Let’s calculate the dot product:
>>> direction.dot(normal)
# 0.05679064802825451
In my case, this returned a small positive value which means the empty is inside the Suzanne. Now I am gonna move the empty outside the Suzanne and try again:
>>> direction.dot(normal)
-0.15257206931710243
As you can see, now it returns a negative value which means the empty is indeed outside.
We can package this up into a handy function that we can use over and over when needed:
import bpy
def is_inside(point, obj):
_point = point - obj.location
_, closest, nor, _ = obj.closest_point_on_mesh(_point, )
direction = closest - _point
if direction.dot(nor) > 0:
return True
else:
return False
If you notice, in the function above, we calculate the coordinates of the point in object space and store it in an internal variable called _point before doing anything else. This way, we can simply pass points in the world space as usual and still get the correct result. We simply check if a point is inside or outside like:
>>> obj = bpy.data.objects["Suzanne"]
>>> point = bpy.data.objects["Empty"].location
>>> is_inside(point, obj)
# True
So, this is how we can check if a point is inside or outside a mesh. Try this function by moving the empty around and see how accurate the function is, especially in tricky scenarios like the ears of the Suzanne where there is a lot of small details.
Conclusion
This function can be applied to other problems like point cloud generation, where you can to place a bunch of point within a mesh volume and so on.
That’s it for now! 🙌🏻
Do you know any other method to determine if a point is inside or outside? Do you think we could done this better or simpler? Or do you any other feedback or thought you would like to share?
Let me know by simply replying to this email or on Twitter. Would love to have a conversation.
P.S
If you have been wondering, looking at the #5, where the other Blender Python Bites are, I have posted them only on Twitter. Apart from tweeting them short, I am planning to write corresponding long form content like this one.
Subscribe to my newsletter
Join 1200+ Technical Artists, Developers and CG enthusiasts who receive my latest posts on Blender, Python, Scripting and Computer Graphics directly to their inbox.
